Solve x/22y/3=1 and xy/3=3using substitution and elimination method Substitution Method in Algebra!HELP PLZ!To solve it by elimination method, let us multiply second equation by 3 3x — 3y = 3 equation 3 Now add first and third equation 5x = 15 x = 3 From equation 2, y = x1 y = 2 Hence x = 3, y = 2 (b) 3x y = 10 Since we have one equation and 2 variables, it cannot be solved by elimination method To solve this, we can go for trial and errorIn particular I am having some trouble on two of the problems 1) Let R be the region between y= 2x and y= x^2 Set up and evaluate the integral necessary to compute the volume when R is rotated about the given line using the given method Line = y= 1 Method = Shells 2)Let R be the region between y= 2x and y= x^2
Http Www Monroe K12 Ky Us Userfiles 997 Classes 1535 Chapter 4 Pdf
2x+x-y/6=2 x-2x+y/3=1 by elimination method
2x+x-y/6=2 x-2x+y/3=1 by elimination method-2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equati5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 ×




Cbnst 1 Science Software Equations
Get an answer for 'x2y=1 2xy=8 find x and y' and find homework help for other Math questions at eNotesGaussian Elimination means that the augmented matrix should be reduced to a triangular matrix, and then How To Solve Equation By Elimination 2x4y=4 3x2y=18?2x – 3y = – xy asked in Linear Equations by Anika01 ( 571k points) pair of linear equations in two variables
Use the elimination method 1) 3xy=1 5xy=9 2) 4x6y=24 4xy=10 3)2xy=3 x3y=16 4) 2x3y=7 3x4y=10 1 See answer mandaa97 is waiting for your help Add your answer and earn pointsSolve the system 2xy=2,3x2y=5 algebraically (1) Method I;The elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first
Elimination method x2y=2x5, xy=3 \square!Write down the steps involved in the elimination method Step 1 At first, we select a variable which we want to eliminate from the equations Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients of theSolve the following simultaneous equations using elimination method 3x 4y 5 = 0 , y = x 4 Solve for x and y, using substitution method 2x y = 7, 4x 3y 1 =0 Solve the following pairs of equation by elimination method x y = 6 2x 3y = 4




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community
👍 Correct answer to the question Solve using the elimination method –x – y = 8 2x – y = 1 eeduanswerscomSolve equation x2y=1 2x3y=12 by using elimination method rohitrajak35 rohitrajak35 Math Secondary School answered Solve equation x2y=1 2x3y=12 by using elimination method 2 See answers cuteboysk cuteboysk Here it is the answer JackelineCasarez JackelineCasarezGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Ii X 2 2y 3 1 And X Y 3 3 Sarthaks Econnect Largest Online Education Community



Http Mrsk Ca Ap 1 4elimination Pdf
X/2 2y/3 = 1 and xy/3=3 Find x and y values using Elimination and Substitution method x/2 2y/3 = 1 and xy/3=3 Find x and y values using Elimination and Substitution methodSolve Following Equation By Elimination Method 3x 2y 11 2x 3y 4 For more information and source, Solve The Following Pairs Of Equations By Reducing Them To A Pair Of Linear Equations 5 X Y 2 X Y 1 Brainly In For more information and source, see on this link httpsSolution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0




Solve X Y 7 And 3x 2y 11




Do Now Solve Each System Using Elimination 2x 3y 8 X Y 2 Ppt Video Online Download
3x3y=21,2xy=12 To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 3x3y=21 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign 3x=3y21Hi, you may find many different solutions but this is the simplest but check the answer first and then follow my steps xy/xy =2 xy/xy =6xy=2xy (1) xy=6xy (2)Add 1 and 22x=8xy2=8yY=1/4 Think You Can Provide A Better Answer ?= 34 x – y = 2 Mathematics Use Elimination Method To Solve This Simultaneous Equation 5V=113U 2U7V=3




Cbnst 1 Science Software Equations



Http Www Monroe K12 Ky Us Userfiles 997 Classes 1535 Chapter 4 Pdf
Steps Download Article Write down both of the equations that you'll need to solve Number the equations 3x y = 12 as number one, and 2x y = 13 as number two Check if both equations have the same variable/unknown term in them Look forBy eliminating x in the expression x y = 1, we get x = 1 −y, which we can plug in the second expression 2(1 −y) − y = − 2 2 − 2y −y = −2 2 − 3y = −2 −3y 2 = − 2 −3y = − 4 y = 4 3 Knowing y, we can now find x by plugging the y value into any of the above equationsAnswer to Solve by the elimination method 3x y = 1;




Math 163 Online Problems Supplemental Lessons On Gaussian
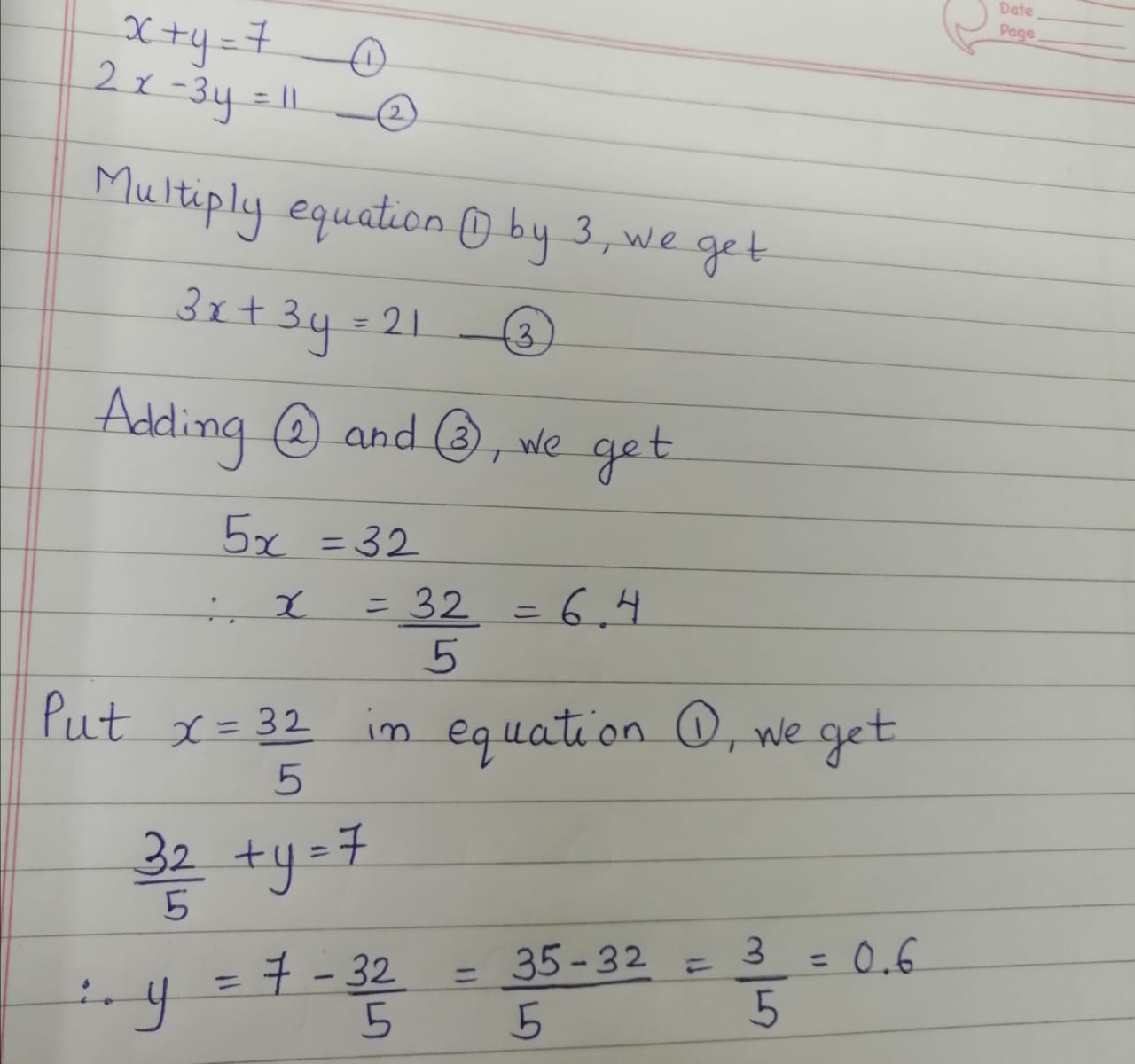



X Y 7 2x 3y 11 Gkvi0xxx Mathematics Topperlearning Com
Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 ×Answer to Solve using the elimination method 2x 3y = 2, 4x 6y = 4 By signing up, you'll get thousands of stepbystep solutions to your#2x y = 1# To solve using elimination, all we do is literally subtract the bottom line from the top line which gets rid of the y #(yy = 0)#, giving us #x = 2# #x = 2# We then substitute (#x =2#) into either of the equations #x y = 1# #(2) y = 1# #y = 3# And then check that this works, using substituting both values into the second equation #2x y = 1#




Answered Question 1 A Discuss Or Outline Bartleby
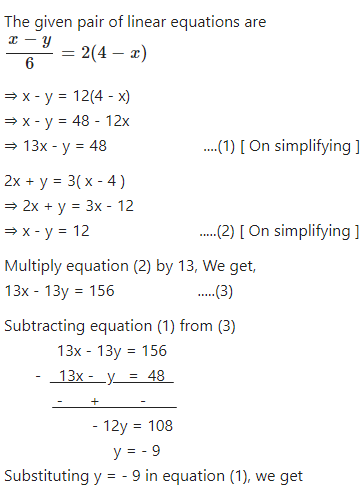



Simultaneous Linear Equations Class 9th Concise Selina Icse Maths Icsehelp
Solve the system using method of elimination x' = x 2y y' = x y with the initial conditions x(0) = y(0) = 1 Get more help from Chegg Solve it with our calculus problem solver and calculatorX2y = 1 Multiply both sides of the equation by 2 to eliminate the y varaible 4x 2y = 6 x 2y = 1 Add 5x = 5 Solve for x and substitute into one of the original equations to find y x = 1 (2y = 3) y = 1 check your answers using one of the equations Solve a system of equations by substitutionSolve the Given equation in Elimination method and Substitution Method




Answered Q1 Find The Values For X Y Z For Bartleby
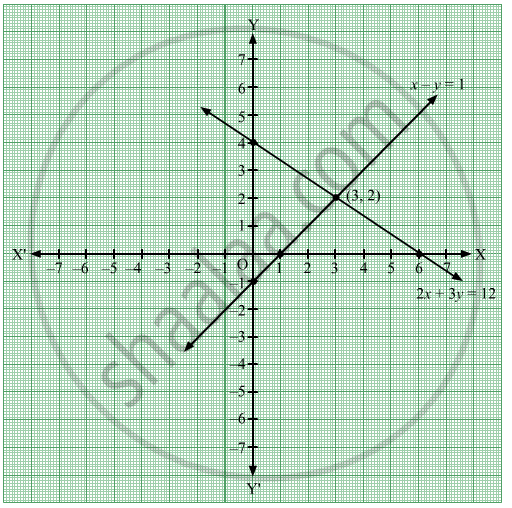



Solve The Following Simultaneous Equation Graphically 2x 3y 12 X Y 1 Algebra Shaalaa Com
Solve by Frobenius Method $$x(1x)y''2(12x)y'2y=0\,$$ The first solution I am able to get is $\dfrac{1}{1x}$ Other solution is $\dfrac{1}{x}$, but I am getting $\dfrac{1}{x(1x)}$ Where am I going wrong?Y=1Stepbystep explanationlet x y=2 (1)2xy=1(2)add (1)(2) 3x=3hence, x=1from (1), y= 21 =1 hence values of x and y are 1 and 1 respeThe elimination method is one of the techniques to solve the system of linear equations In this method, either add or subtract the equations to get the equation in one variable If the coefficients of one of the variables are the same, and the sign of the coefficients are opposite, we can add the equation to eliminate the variable




Page Date Solve Pair 2 Cg23 B See How To Solve It At Qanda




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
Solve the equations using elimination method3x2y = 7 and 4x−3y = −2 Solve the equations using elimination method 3Substitution Solve the first equation for y 2xy=2 Subtract 2x from each side to get y=2x2 Now substitute this expression for y(2) –x = –3 x = 3 Putting x = 3 in equation (1) x – y = –2 3 – y = –2 –y = –2 – 3 –y = –5 y = 5 So, x = 3, y = 5 is the solution of our equation ∴ Numerator = x = 3 &




Mathematics 8 Systems Of Linear Inequalities



Use Gauss Jordan Method To Solve Nbsp X Y Z 9 2x 3y 4z 13 3x 4y 5z 40
You can do this by simply adding the two left sides and the two right sides separately like this Group like terms Combine like terms Simplify Divide both sides by to isolate Reduce Now go back to the first equation Plug inX 8y = 42 By signing up, you'll get thousands of stepbystep solutions to your homeworkThe elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable cancels out Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy
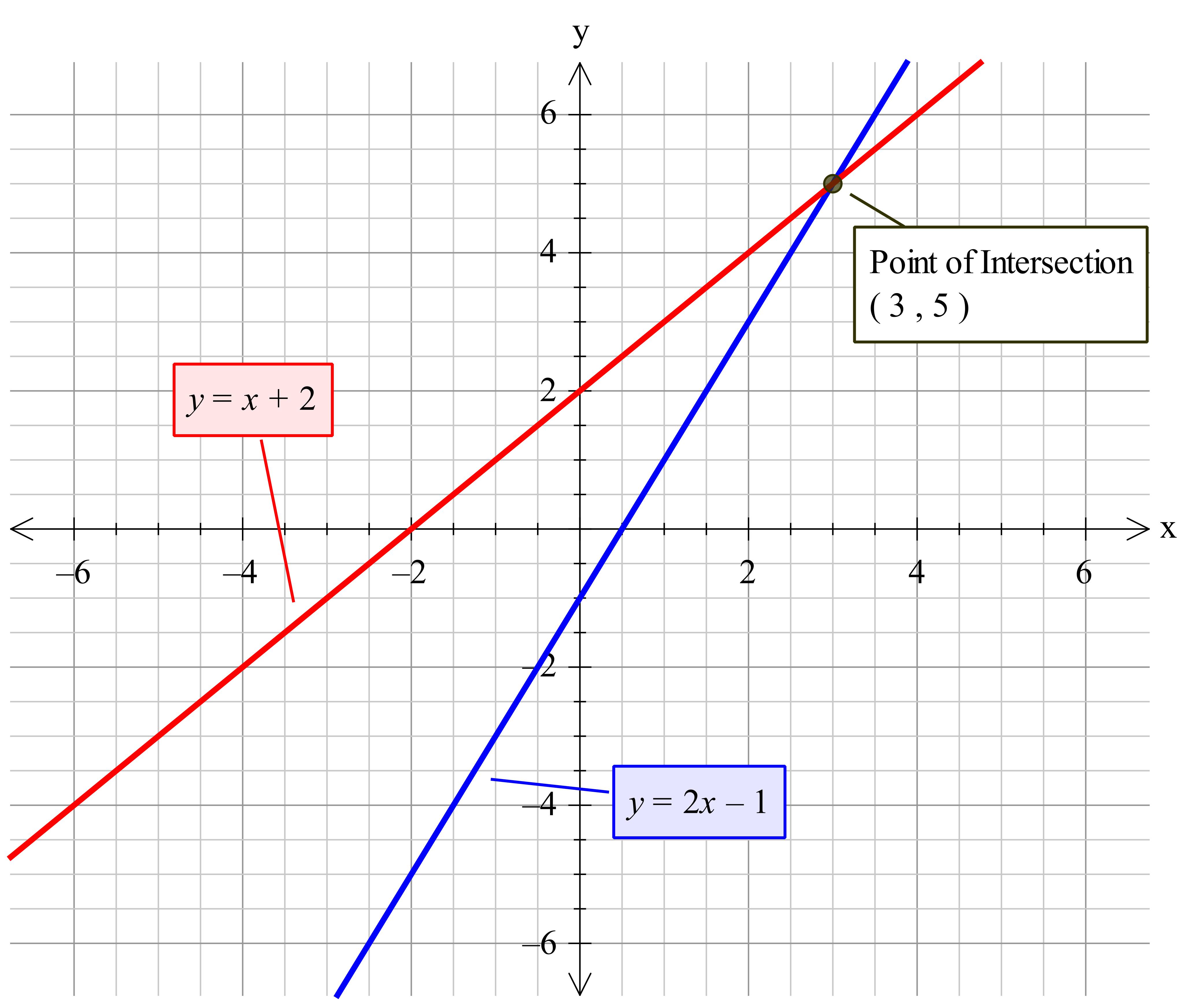



How Do You Solve Y 2x 1 And Y X 2 Socratic
Example 4 Solve the system of linear equations using the GaussJordan elimination method 7x 2y 1 3x y 1 − − =− = Question 5 Is the following matrix row reduced?In the elimination method, you first multiply the constant with the help of a constant There are two ways in which you can solve a linear equation One is by plotting a graph of the equations, and in the other one, you solve the equations through the elimination method Solving a Set of Linear Equations By the Elimination MethodSolve the simultaneous equation using substitution method4x = y 7and 3x 4y 9 = 0 Math 3 Solve the simultaneous equations x²




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Ex 3 4qno1 1 Solve X Y 5 2x 3y 4 By The Elimination Method Youtube
About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or subtracting your equations together You can use this Elimination Calculator to practice solving systemsThe taxi fare in city is as follows For the first kilometer , the fare is Rs and for the subsequent distance it is Rs9 per km Taking the distance covered as x km and total fare as Rs y , write a linear equation for this information , and draw its graph , find the fare ,Mathematics To eliminate y, double the second equation and add it to the first 2(3x 2y) (2x 4y) Xyz=5 2y3z=14 3y2z=5 solve the system useing any algebraic method?



Solved 9 Solve The Following System Of Linear Equations Using The Gauss Jordan Elimination Method For The Variable Y Xty 1 3x 2y 0 2x Y Course Hero




Lo I Can Solve Simultaneous Equations Date
Solve the following systems of linear equations by Gaussian elimination method (i) 2x – 2y 3z = 2, x 2y – z = 3, 3x – y 2z = 1 ← Prev Question Next Question → 0 votesSolve this question with the elimination method X 2y = 4 Y = x 2 Get the answers you need, now!Denominator = y = 5 Hence, Original Fraction




Slove The Substitution Method X Y 5 X Y 1 Brainly In




Solve The Following System Of Equations 5 X 1 2 Y 1 1 2
Solve each pair of simultaneous equations by elimination method x 2y = 8 x y= 6 Given, x 2y = 8(i) x y = 6(ii) By elimination method, Subtracting (i) and (ii) x 2y = 8 x y = 6 or, y = 2 So, y = 2 Then, x 2 = 6 So, x = 4 2x y = 13 x – y= 2 Given, 2x y = 13(i) x – y = 2(ii) By elimination methodLet's explore a few more methods for solving systems of equations let's say I have the equation 3x plus 4y is equal to 25 and I have another equation 5x 5x minus 4y is equal to twenty five point five and we want to find an x and y value that satisfies both of these equations if we think of it graphically this would be the intersection of the lines that represent the solution sets to both of5 − 6)/5 x = (25 −




Solve For X And Y 2x Y 3 0 3x 7y 10 0



Www Marlboroschools Org Cms Lib Ny Centricity Domain 196 Integrated algebra Regents review Linear systems Solving systems by elimination Pdf
Use the Substitution method to solve the system of equations 3x y = 5 4x 7y = 10 multiply first equation by 4 multiply second equation by 3 thus both equations have same x or y value in this case it is the x value 12x 4y\(x y = 5 \\2x 3 y= 4 \) Steps Elimination methodSystemofequationscalculator elimination method x2y=2x5, xy=3 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables In this blog post,




Linear Equations In Two Variables




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
Solve by Addition/Elimination xy=2 xy=4 x y = 2 x y = 2 x − y = 4 x y = 4 Multiply each equation by the value that makes the coefficients of x x opposite xy = 2 x y = 2 (−1)⋅(x −y) = (−1)(4) ( 1) ⋅ ( x y) = ( 1) ( 4) Simplify Tap for more steps Simplify ( − 1) ⋅ ( x − y) ( 1) ⋅ ( x𝑁𝑢𝑚𝑒𝑟𝑎𝑡𝑜𝑟/(𝐷𝑒𝑛𝑜𝑚𝑖𝑛𝑎𝑡𝑜𝑟 1)=1/2 𝑥/(𝑦 1)=1/2 2x = y 1 2x – y = 1 Hence, our equations are x – y = –2 (1) 2x – y = 1 (2) We use elimination method with equation (1) &Elimination method First multiply one or both the equations by some suitable nonzero constants to make the coefficients of one variable numerically equal then add or subtract one equation from the other so that one variable gets eliminated (i) What is the Known?




Solved By Elimination Method 2x Y 5 And 3x 2y 8 Brainly In




Solve X Y 2x Y 6 2x Y 2 By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
1 Solve the system using substitution method 2x y = 2 5x 3y = 9 2 Solve the system using elimination or addition method 11x = 5 – 4y 2(x – 2y) = 22 y 3 Solve the system by the method of your choice 4x y = 0 3y z = 1 4x z = 12 4 Solve the system using elimination method 2x2 3y2 = 11 x2 4y2 = 81 1 0 −5 0 0 1 3 a Yes b NoSolve the following system of equations by elimination method x y = 7xy;




Example 12 Use Elimination Method 2x 3y 8 4x 6y 7



Solution Solve By Using Elimination Method 4x 2y 3 2x Y 1 Separate Problem 2x Y 1 X Y 3
Solve by Addition/Elimination xy=1 xy=3 Multiply each equation by the value that makes the coefficients of opposite Simplify Tap for more steps Simplify Tap for more steps Apply the distributive property Rewrite as Multiply Tap for more steps Multiply by Multiply by




Solve The System Graphically And By Hands X 2 Y 2 Chegg Com




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Practical Exercises 3 System Analysis




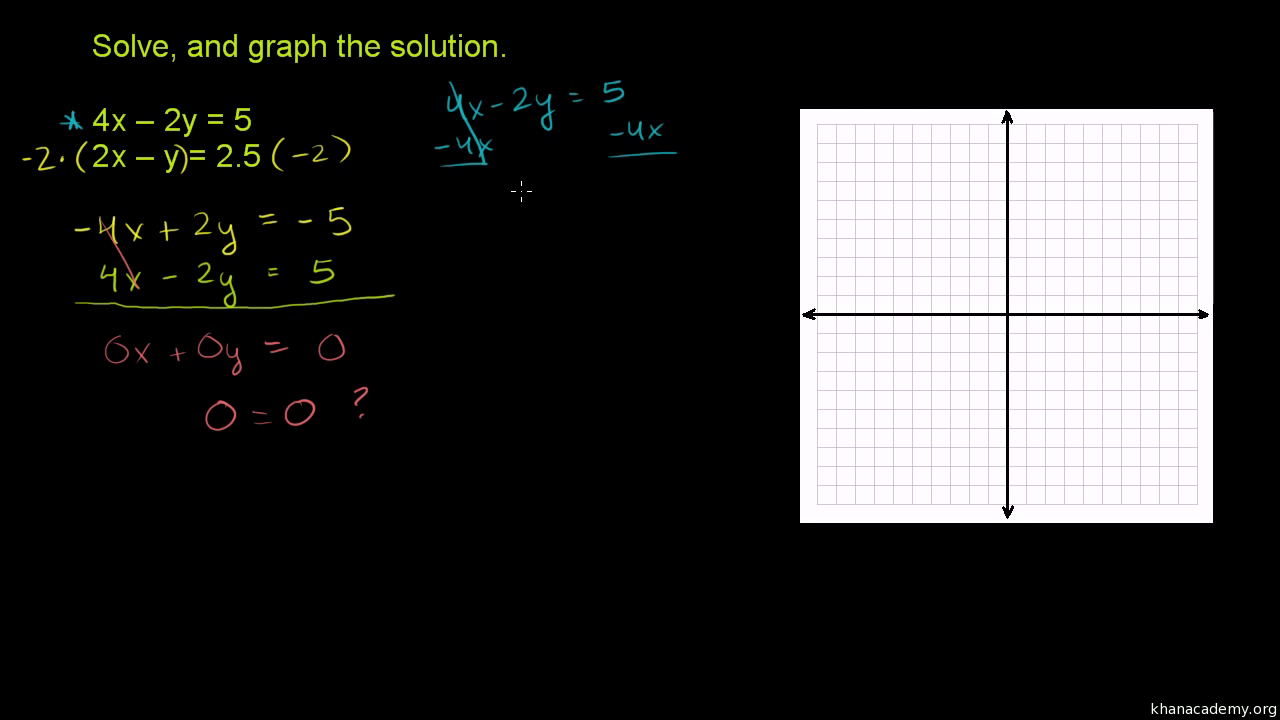
Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora



16 X Y 2 X Y 1 8 X Y 12 X Y 7 Find The Value Of X And Y Quora




Solved X Y 0 2x Y 9 By Elimination Brainly In




Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables




5 41 5 0 6 30 Solve Each System Using Gaussian Chegg Com
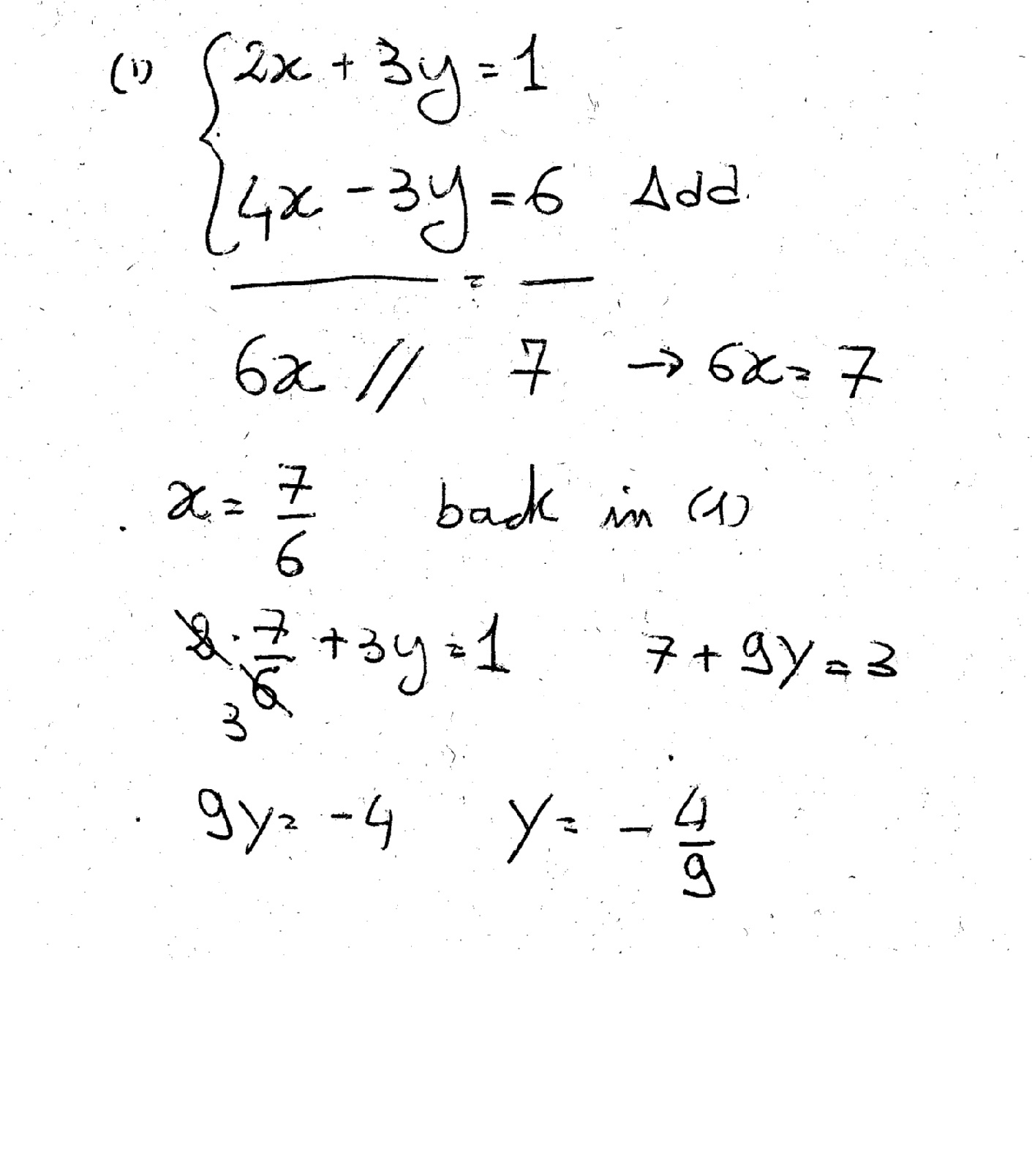



How Do You Solve The System Using The Elimination Method For 2x 3y 1 And 4x 3y 6 Socratic




Solve For X And Y 2x Y 6 And X Y 2 Brainly In




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Solve The Given System Of De By Elimination Method 3 D 2 X Y Homeworklib
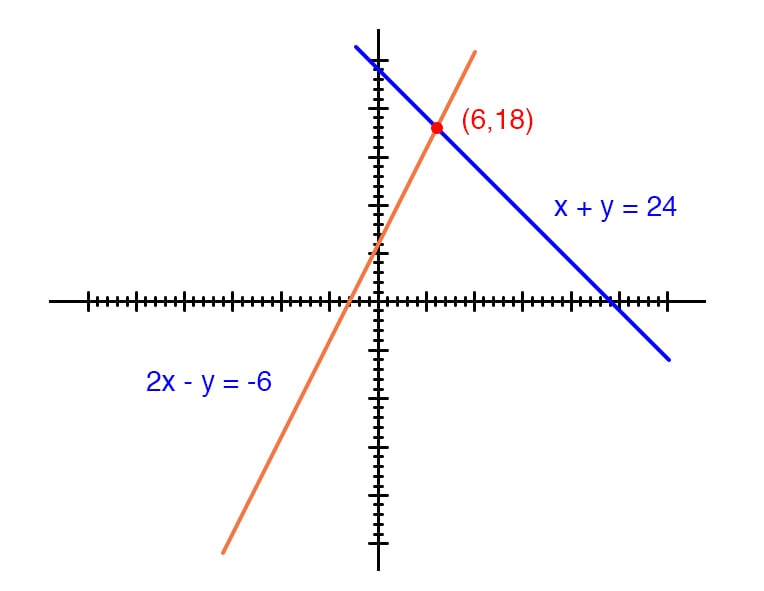



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook



Systems Of Linear Equations




Mathpowerblog How To Do The Math




Exercise 1 6 Matrix Non Homogeneous Linear Equations Problem Questions With Answer Solution
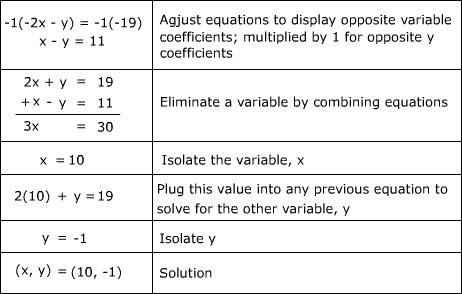



Solving Systems Of Equations By Elimination Quiz



Ncert Solutions For Class 10 Maths Pair Of Linear Equations In Two Variables




X4y 2 5 Xy 6z 12 3x Y Z4 See How To Solve It At Qanda



If X Y 3 X Y 1 Then What Is X Y Quora




X 3y 7 2x Y 1 0 Novocom Top




Solve 2x Y 5 And 3x 2y 8




2x Y 11 And X Y 8 Solve Using Substitution And Elimination Method Youtube




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Chapter 9 Systems Of Linear Equations Pdf Free Download




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




Solve 2x Y 1 X Y 2 By Elimination Method Brainly In




C 2times Y3 4xy 3 D 2tim See How To Solve It At Qanda
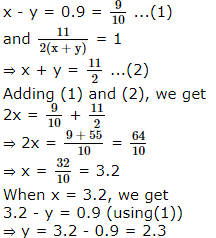



The Solution Of The Equation X Y 0 9 And 11 2 X Y 1 Isa X 3 2 Y 2 3b X 2 3 Y 3 2c X 1 0 Y 0 1d X 2 Y 1 1correct Answer Is Option A Can You Explain This Answer Edurev Upsc Question




Slove By Substitution Method X Y 2 2x Y 1 Brainly In




Chapter 9 Systems Of Linear Equations Pdf Free Download




2x Y 8 X Y 5 Elimination Method Novocom Top




I Solve The Following System Of Linear Equations Chegg Com




Ppt System Of Equations And Elimination Powerpoint Presentation Free Download Id




Solve The Given Pairs Of Linear Equations By Using Elimination Methods 1 3x 4y 10 And X Y 1 2 Brainly In




Solve These By Elimination Method 1 2x Y 4 And 5x 3y 1 2 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Solve By Elimination Method X Y 6 X Y 4 Maths Linear Equations In Two Variables Meritnation Com




36 X Y 2 3x Y 35 X Y 5 2x Y 12 65 37 2x Chegg Com




2x 3y 12 X Y 1 Simultaneous Novocom Top



Solve X Y 11 And 2x Y 19 By Elimination Youtube



Simultaneous Equations




Solve Each Other Pair Of Equation Given Below Using Elimination Method 3 X 2 Y 9 Xy 9 X 4 Y 21 Xy Mathematics Topperlearning Com 59bn37qq




Solve Each With Substitution 2x Y 6 Y 3x 5 3x 4y 4 Y 3x Ppt Download




Use Gaussian Elimination Method To Solve The Chegg Com




Exercise 1 6 Matrix Non Homogeneous Linear Equations Problem Questions With Answer Solution



Solve The Following Pairs Of Linear Equations By Elimination Method And The Substitution Method I X Y 5 And 2x 3y 4 Sarthaks Econnect Largest Online Education Community




Elimination Method Day 1 Ppt Download



The Elimination Method
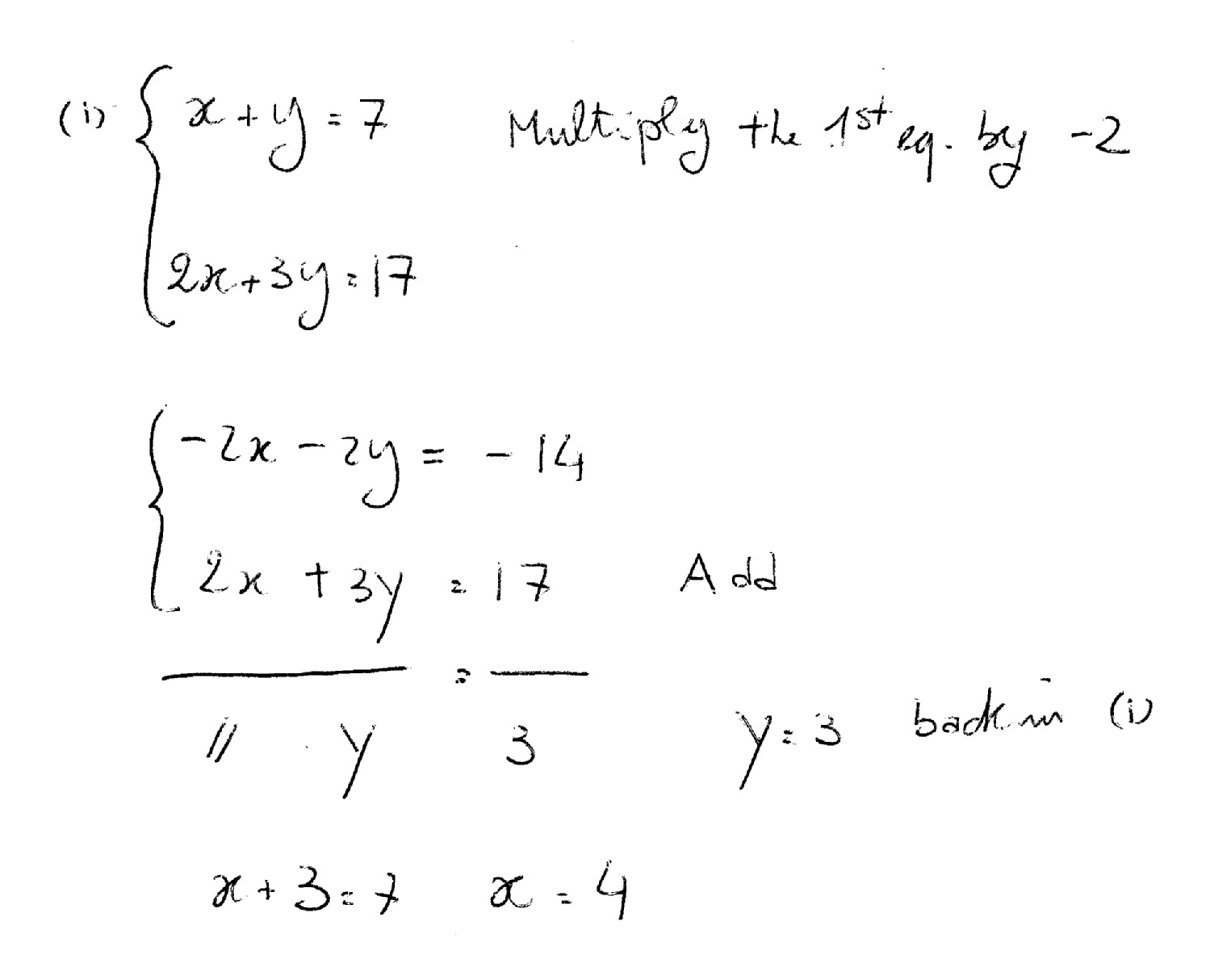



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic




Solve X 2y 1 2x Y 7 Maths Questions



Use Gauss Jordan Method To Solve Nbsp X Y Z 9 2x 3y 4z 13 3x 4y 5z 40




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection
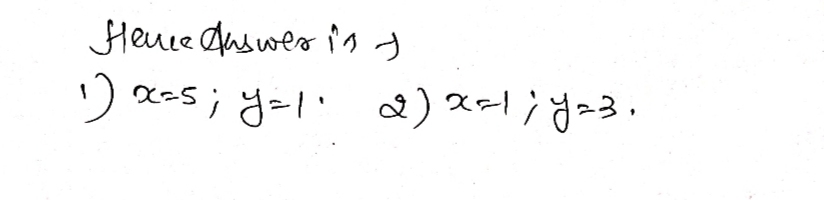



Using Elimination Method 1 2x Y 11 2 X 4y 13 X Y Gauthmath




Elimination Method Day 1 Ppt Download



Using Gaussian Or Gauss Jordan Elimination X Y Z 5 2x 3y 6z 32 4x 5y 10z 8 Mathskey Com




2x X Y 6 2 X 2x Y 3 1 Mathematics Topperlearning Com Fqktm544



2x 3y 12 X Y 1 Graph Sarthaks Econnect Largest Online Education Community




Using Elimination Method 1 2x Y 11 2 X 4y 13 X Y Gauthmath




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




X Y 5 2x 2y 10 Elimination Method Novocom Top




Algebraic Elimination Method Class 10 Ncert Solutions Suresolv
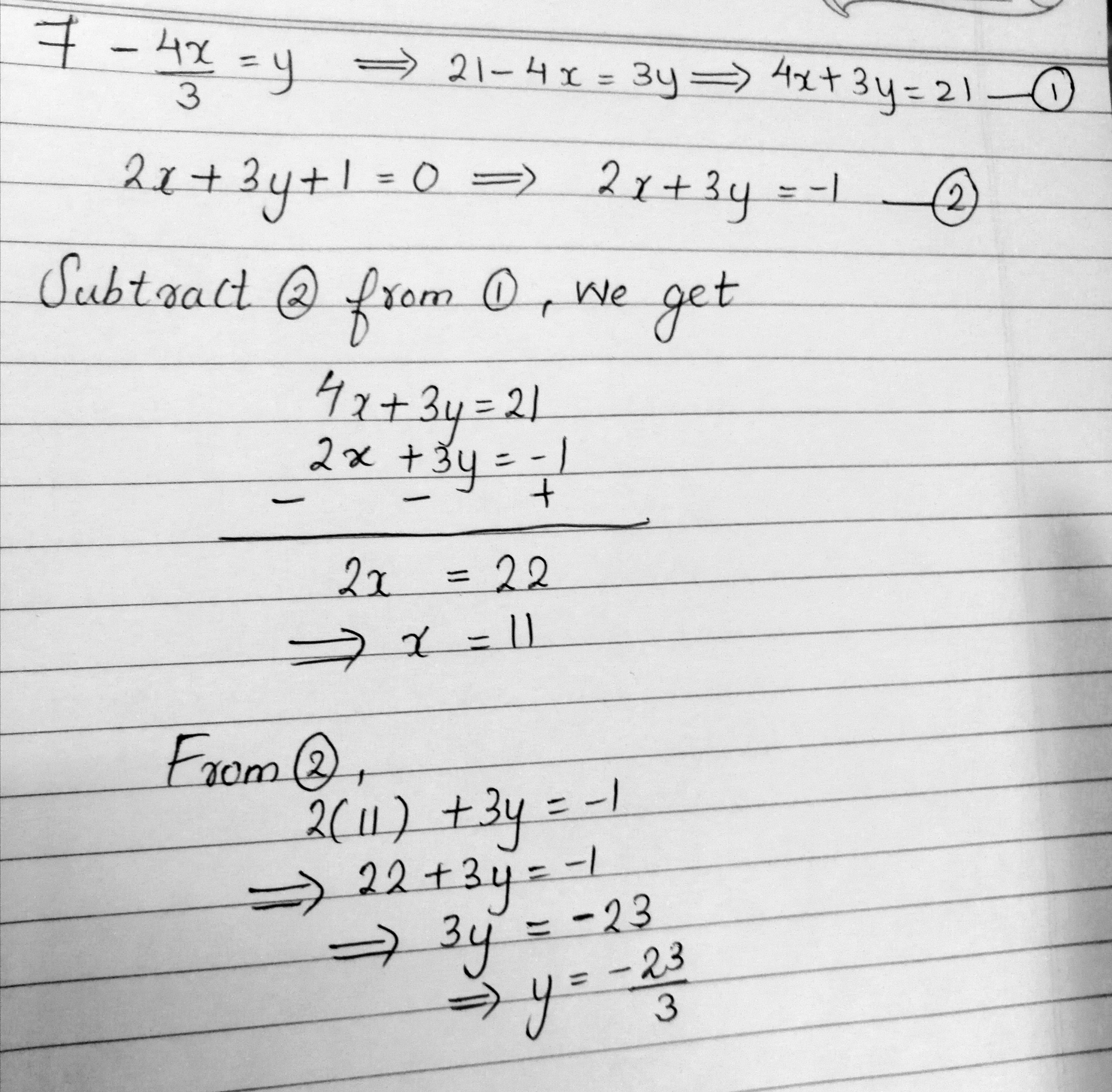



7 4x 3 Y 2x 3y 1 0 Mathematics Topperlearning Com Iwb1egg




Chris Carlson Mathpowerblog




Solve Edl 3 X Y 15 E 2 X 4y Answers 2x Y 7 E9x Y 2x 9 7x 4y 6 E 4x Y 8 X 2y 13 E 5x 14 3y 10 2x 3 12 5y Ci 2y 5x 4 3y 1 8x 5x 2y



0 件のコメント:
コメントを投稿